Подборка задач ЕГЭ по стереометрии

ЕГЭ по математике предполагает умение решать задачи по стереометрии. Данные задачи не трудны, но тем не менее необходимо готовиться, чтобы смочь данные задачи. В данной заметке рассмотрим задачи, решение которых поможет подготовиться к решению задачи C4.

Также отмечу, что при решении задач по стереометрии будущий выпускник готовится также и для решения задачи C2 по планиметрии, которая традиционно является одной из двух самых трудных задач в ЕГЭ по математике.

Задачи по стереометрии

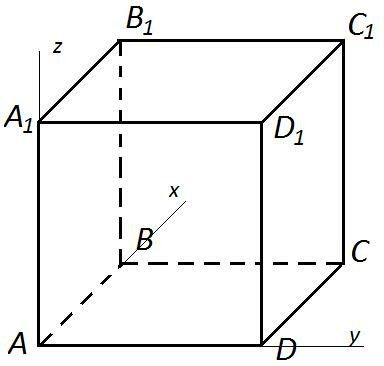
1. Дан куб с основанием ACBD и боковыми ребрами AA₁, BB₁, CC₁, DD₁. Длина всех ребер куба равна 1. Точки M и N – середины ребер CD, CC₁. Найти расстояние между прямыми AN и BM. Ответ: .

2. Сфера проходит через вершину A куба  ABCDA₁B₁C₁D_1, середины ребер AB и AD, касается грани  A₁B₁C₁D₁. Найти отношение площади поверхности сферы к площади полной поверхности куба. Ответ:

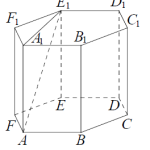
3. Основание BC равнобедренной трапеции ABCD и сторона BC ромба MBCN совпадают, причем BC=a, AD=b (a<b<2a). Найти площадь поверхности тела, образованного совместным вращением трапеции и ромба вокруг прямой, содержащей BC, если острый угол трапеции равен 30 градусов, а острый угол ромба равен 60 градусов.

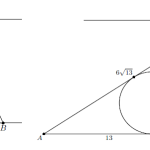
4. В пирамиде ABCD ребра AC, BC, DC попарно перпендикулярны и AC=BC=LC=4. Точка N – середина ребра AB, а точка M расположена на ребре AD так, что AM:MD=3. Шар с центром на прямой CN касается ребра AD в точке M. Найти радиус шара. Ответ:

5. В условиях первой задачи определить угол между указанными прямыми.

Для решения задачи 5 в данном случае удобно воспользоваться методом координат. В данном случае проведем оси как показано на рисунке. Тогда точки будут иметь следующие координаты:

A (0;0;0), B(1;0;0), M(0,5;1;0), N(1;1;0,5).

Отсюда находим, что координаты векторов AN и BM имеют вид

AN=(1;1;0,5)  BM=(-1;1;0)

Далее учитываем, что угол между прямыми – это угол между направляющими векторами этих прямых. Поэтому используя два способа нахождения скалярного произведения, находим косинус искомого угла. До чисел не довожу, вроде все понятно.

Если есть вопросы, готов более подробно рассмотреть решение.