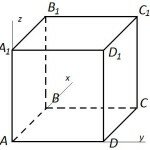
- Дан куб с основанием ABCD боковыми ребрами AA1, BB1, CC1, DD1. Длина ребра куба равна 1. Через прямую B1C проведена плоскость, пересекающая ребро AB и составляющая угол 60° с прямой A1B. В каком отношении эта плоскость делит ребро AB?
Ответ: 1:1. - Вершины куба с ребром 1 являются центрами шара одинакового радиуса. Объем части куба, расположенной вне шаров, равен ½. Какая часть ребра куба лежит вне шаров?
Ответ: 1-(3/π)1/3 - Ребро куба ABCDA1B1C1D1 равно a. Найти радиус сферы, проходящей через середины ребер AA1, BB1 и через вершины A, С1?
Ответ: a√14/4 - Двугранный угол при боковом ребре правильной треугольной пирамиды равен 2α. Высота пирамиды равна h. Найдите объем конуса, описанного около пирамиды.
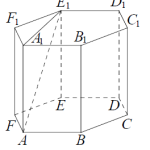
Ответ: 1/3πh3(3 tg2-1) - Дана прямая призма ABCA1B1C1 , стороны основания которой AB=BC=1, AC=√3. В каком отношении объем вписанного в призму цилиндра делится плоскостью A B1C ?
Решение: Пусть K – точка пересечения плоскости A B1C с осью цилиндра, тогда отношение, в котором делится объем цилиндра плоскостью A B1C, равно отношению, в котором делится его ось точкой K.
Ответ: √3/2. - Высота пирамиды равна 5, а основанием служит треугольник со сторонами 7, 8 и 9. Некоторая сфера касается плоскостей всех боковых граней пирамиды в точках, лежащих на сторонах основания. Найти радиус сферы.
Решение: Основанием высоты пирамиды служит центр вписанной в основание пирамиды окружности, центр сферы лежит на продолжении высоты пирамиды.
Ответ: √6.




Последние комментарии