Факты из геометрии для решения заданий C4 ЕГЭ по математике

Приведу некоторые утверждения, которые полезны при решении геометрических задач. Особенно полезен данный материал будет при подготовке к ЕГЭ по математике. Приведены не стандартные факты. Для полноты картины смотрите также факты по ортоцентру треугольника.

Треугольник

•  В треугольнике со сторонами a, b, c расстояние от вершины А до точек касания вписанной окружности сторон, содержащих эту вершину, равно (b+c-a)/2
• Пусть окружность касается стороны BC треугольника ABC и продолжений сторон AB и AC. Тогда расстояние от вершины A до точки касания окружности с прямой AB равно полупериметру треугольника ABC.
• Медиана треугольника разбивает его на два равновеликих треугольника.
• Если у двух треугольников равны высоты, то их площади относятся как основания.
• Прямая, параллельная стороне треугольника и пересекающая две другие, отсекает от него треугольник, подобный данному.
• Высоты остроугольного треугольника являются биссектрисами его ортотреугольника (треугольник, образованный основаниями высот).

Четырехугольники

• Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали – полусумме оснований (средней линии).
• Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник
• Трапеция вписана в некоторую окружность тогда и только тогда, когда она является равнобедренной.
• Центр окружности, описанной около трапеции, лежит на пересечении серединных перпендикуляров к сторонам трапеции.
• Диагональ параллелограмма разбивает его на два равновеликих треугольника.
• Трапеция разбивается диагоналями на два равновеликих треугольника (примыкающих к боковым сторонам) и два подобных треугольника (примыкающих к основаниям).

Окружности

• Радиус (диаметр), перпендикулярный хорде, делит хорду пополам.
• При любом способе касания точка касания и центры окружностей лежат на одной прямой.
• При внешнем касании центры окружностей расположены на линии центров по разные стороны от точки касания, при внутреннем – по одну сторону.
• Расстояние между центрами касающихся окружностей радиусов R и r ( R≥r) равно R +r при внешнем касании и R -r при внутреннем.
• Пересекающиеся окружности в точках А и В имеют общую хорду АВ. Общая хорда перпендикулярна линии центров и делится ею пополам.
• Вписанный угол измеряется половиной дуги, на которую он опирается.
• Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
• Если через точку A, лежащую внутри окружности, проведены две хорды MN и KL, то MA·AN=KA·AL.
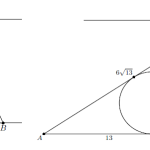
• Если из точки A, лежащей вне окружности, проведены касательная AB и секущая AD, то AB²=AD·AC.
• Длины двух касательных, проведенных из одной точки к заданной окружности, равны между собой.
• Равные хорды окружности равноудалены от ее центра, и наоборот равноудаленные от центра окружности хорды равны.

Постовой. Вы хотели узнать об элитных домах более подробно? Воспользуйтесь предложение от коттеджного поселка Чехово.