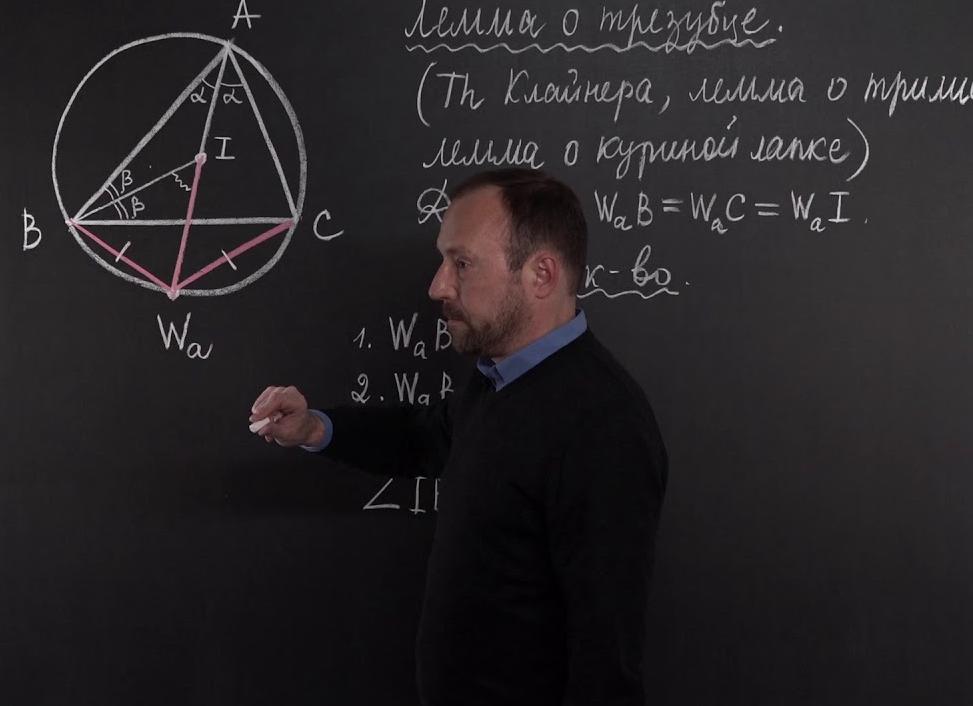Лемма о трезубце, она же лемма о трилистнике, лемма о куриной лапке и теорема Мансиона. Сейчас я приведу формулировки и доказательства этой теоремы. В силу того, что этой леммы нет в учебниках, её нельзя использовать без доказательства, а в задании 17 ЕГЭ профиль вам могут дать задачу, использующую идеи этой теоремы. Так что важно будет разобрать и понять доказательство тем, кто хочет побороться за высокие баллы.
Вокруг треугольника АВС описана окружность с центром в точке О. Точка I —центр вписанной окружности. Продолжение биссектрисы BI пересекает описанную окружность в точке F. Отрезки AF, IF и FC равны.
AI, BI и CI — биссектрисы углов А, В и С соответственно. Обозначим половину угла А как α, а половину угла В как β. Так как BI — биссектриса угла B, то ∠ABF=∠СBF=β, а значит будут равны и хорды AF и CF, на которые опираются эти вписанные углы. ∠CAF = ∠СBF=β, как вписанные углы, опирающиеся на одну хорду. ∠FAI = ∠FAC + ∠CAI = α+β. ∠AIF = ∠BAI + ∠ABI = α+β как внешний угол треугольника AIB, то есть равен углу FAI, а значит треугольник FAI — равнобедренный. Следовательно AF=FI=FC. Чтд.
Обобщённая лемма о трезубце.
Вневписанная окружность с центром в точке I1 касается стороны АС. FI1=FI=FA=FC.
Как мы знаем из курса планиметрии, центр вневписанной окружности лежит на пересечении биссектрисы внутреннего угла треугольника и биссектрис двух внешних углов. Попробуйте воспроизвести доказательство.
Теперь вспомним другой геометрический факт. Угол между биссектрисами смежных углов равен 90°. Попробуйте доказать этот факт.
Построим биссектрисы угла А и внешнего угла при вершине А. Угол между этими биссектрисами равен 90°. Построим биссектрисы угла В и внешнего угла при вершине В. Угол между этими биссектрисами равен 90°. Получившийся четырёхугольник AICI1 можно вписать в окружность, так как сумма противоположных углов равна 180° (∠IAI1 + ∠ICI1 = 180°).
Кроме этого по лемме о трезубце мы знаем, что AF=FI=FC, а значит эти отрезки являются радиусами описанной около треугольника AIC окружности с центром в точке F. А значит эта та же окружность, которая описана около четырёхугольника AICI1, следовательно FI1=FI=FA=FC. Что и требовалось доказать.
Постарайтесь самостоятельно воспроизвести доказательство. В таком случае вы, скорее всего, сможете справиться и с задачей на ЕГЭ, которая использует ту же основную идею. Если остались вопросы, то задавайте их в комментариях.
Задача на лемму о трезубце — https://vk.com/valeriyamath?z=video-214545621_4562393..
Подробная информация про курс для учителей — https://vk.com/valeriyamath?w=wall-214545621_500
Записаться на курсы для учителей https://forms.gle/fM9LzHxWECdrCarJ7
Отзывы учителей (https://vk.com/topic-214545621_52185117)