В статье “Демонстрационный вариант ЕГЭ по математике на 2011-й год” сформулирован полный текст задания. В данной статье рассмотрим решение задач B8-B12.
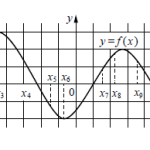
B8. На рисунке изображен график функции y= f(x) и касательная к этому графику в точке с абсциссой, равной 3. Найдите значение производной этой функции в точке x =3.
Решение:
Обозначим две точки касательной через А(3;1) и B(0;-5). Теперь учтем тот факт, что производная в точке равна угловому коэффициенту касательной, проведенной через заданную точку. А далее вспоминаем, что угловой коэффициент прямой равен тангенсу угла наклона, поэтому получаем, что производная равна (1-(-5))/(3-0)=2.
Ответ: 2.
B9. Объем первого цилиндра равен 12 м³. У второго цилиндра высота в три раза больше, а радиус основания – в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
Решение: Пусть высота первого цилиндра равна h, а радиус основания – r. Учитывая, что объем равен 12 м³, получаем выражение 12=π*h*r2, отсюда находим, что π*h*r2=12.
Рассмотрим теперь второй цилиндр, его высота и радиус основания будут соответственно равны 3h, r/2. Вычислим объем второго цилиндра с учетом того, что π*h*r2=12: V=3*π*h*r2/4=h*r2/4=9.
Ответ: 9.
B10. Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой h(t) = −5t2 +18t (h – высота в метрах, t – время в секундах, прошедшее с момента броска). Найдите, сколько секунд камень находился на высоте не менее 9 метров.
Решение: Здесь надо просто решить неравенство −5t2 +18t>=9. Решением неравенства будет отрезок [0,6;3], длина которого равна 2,4, что и будет ответом.
Ответ: 2,4.
B11. Найдите наибольшее значение функции
y=2cos x+√3x-√3π/3 на отрезке [o,π/2]
Решение: Найдем производную функции
y´=-2sin x+√3.
Приравняем ее к нулю. Получаем, что производная равна 0 при
x=(-1)kπ/3+πn.
Отрезку [o,π/2] принадлежит только точка π/3.
Найдем значения в точках 0, π/3, π/2. Убеждаемся что максимум достигается в точке π/3 и равен 1.
Ответ: 1.
B12. Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй – за три дня?
Решение: Пусть первый рабочий выполнит работу за х дней. Второй – за y дней.
Скорость выполнения работы первым рабочим равна 1/x. Вторым – 1/y.
То, что вдвоем могут выполнить работу за два дня, записывается так: 1/x+1/y=1/12.
Второе уравнение имеет вид: 2/x=3/y.
Получили систему из двух уравнений с двумя неизвестными, из которой находим, что x=20.
Ответ: 20.
Связанные статьи
-
Решение задач B1-B7 демонстрационного варианта ЕГЭ по математике 2011
-
Демонстрационный вариант ЕГЭ по математике на 2011-й год
-
Демонстрационный вариант ЕГЭ по математике на 2012-й год
-
Решение демоварианта егэ по математике 2014. b4-b9
-
Решение демонстрационного варианта егэ по математике 2014
-
Решение задач b9, b10, b11 демонстрационного варианта по математике на 2012-й год
27 Май 2011 в 11:23
Я ТОЖЕ ТАК ХОЧУ!!!(((((
9 Июль 2011 в 18:15
В11. Хотелось бы более подробное объяснение
31 Август 2011 в 7:44
Здесь все сделано в соответствии со следующим алгоритмом поиска максимума/минимума функции на отрезке:
1. Находим производную, приравниваем ее к нулю, получаем набор точек.
2. К этому набору добавляем концы отрезка.
3. Находим значения функции во всех точках набора.
4. Выбираем те точки, в которых достигается максимальное или минимальное значение.
9 Июль 2011 в 18:17
и В8. Почему получилось 2? Ведь 3 разделить на 6 = 0,5
31 Август 2011 в 7:38
Это была опечатка. Сейчас исправил.
14 Сентябрь 2011 в 9:12
Почему в В9 число ПИ=1/3 ???
14 Сентябрь 2011 в 11:24
Здесь не ПИ=1/3, а коэффициент ПИ пропущен. 1/3 тоже нужна.
14 Сентябрь 2011 в 11:04
спасибо тебе))))))))
11 Декабрь 2011 в 17:22
А как уравнение 2/x=3/x было решено? Я никак не могу понять, как получилось 20…
11 Декабрь 2011 в 17:33
Второе уравнение другое, а именно
2/x=3/y
Это уравнение вместе с уравнением
1/x+1/y=1/12
составляет систему из двух уравнений с двумя неизвестными. Ее и решаем…
6 Март 2012 в 17:04
V=1/3*π*h*r2 формула объема не целиндра а конуса …
6 Март 2012 в 17:05
*цилиндра
6 Март 2012 в 21:15
Да, недоразумение вышло. Исправил, но я два раза ошибся и получил правильный результат. Спасибо за сообщение об опечатке.
29 Март 2012 в 13:14
В в9 непонятно почему r в квадрате делится на 4. Почему на 4, когда в двое меньше?
29 Март 2012 в 13:49
Если одно число больше другого в два раза, то квадрат этого числа больше квадрата другого числа уже в 4 раза. Можете на конкретных примерах убедиться.
28 Май 2013 в 18:37
Данные решения полезны и тем, кто готовится к егэ по математике в 2013-м году.