Я предлагаю вам ознакомится с решением 26 задачи части С из гиа по математике на тему: Комбинация многоугольников и окружностей
№1.
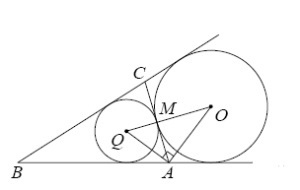
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC в его середине . Найдите радиус окружности, вписанной в треугольник ABC.
Решение:
1) Возьмем Ох за центр данной окружности. Q – это центр окружности вписанной в треугольник ABC.
2) AC делится пополам точкой касания M. AQ и AO – биссектрисы смежных углов, а значит угол OAQ прямой.
3) Из прямоугольного треугольника OAQ получим AM^2=MQ x MO.
4) Значит, QM=AM^2/OM=36/8=4.5
Ответ: 4.5
№2.
Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Решение:
1) Отрезок B1C1 проходит через центр описанной окружности, значит B1C1 является диаметром.
2) Углы BB1C, CC1B и CAB – вписанные и опираются на одну и ту же дугу, следовательно, они равны.
3) Прямоугольный треугольник B1OC. В нем угол B1OC=90 градусов – угол BB1C.
4) Прямоугольный треугольник LCO. В нем угол LCO=90 градусов- угол B1OC и равен углу BB1C и углу BAC.
5) Рассмотрим прямоугольный треугольник CAM. Углы BAC и ACC1 равны, а значит угол BAC= углу ACC1=90 градусов/2=45 градусов.
Ответ: 45 градусов.
№3.
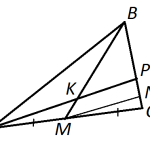
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ = 14, SQ = 4 .
Решение:
1) Поскольку угол QPS = углу QPM = углу MNQ = углу QNP , а треугольник PQS подобен треугольнику NQP по двум углам, потому что у них угол при вершине Q общий.
2) Следовательно QS/PQ=PQ/QN. Возьмем NS за х. Тогда 4/14=14/x+4
3) Получаем, что х=45
Ответ:45






Последние комментарии