В статье “Демонстрационный вариант ЕГЭ по математике на 2012-й год” приведены все задания демонстрационного варианта. В данной статье рассмотрим решение задач b5-b8.
B5. Найдите корень уравнения 
Решение. 
Ответ. 12
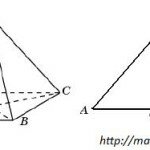
B6. Треугольник ABC вписан в окружность с центром O . Найдите угол BOC , если угол BAC равен 32° .
Решение. Сделаем рисунок. Обратим внимание на то, что углы BOC и BAC опираются на одну дугу. Но при этом точка A находится на окружности, а точка O – центр окружности. На основании известной теоремы получаем, что угол BOC в два раза больше, чем угол BAC, т.е. равен 64° .
Ответ. 64° .
B7. Найдите sinα , если cosα = 0,6 и π <α <2π.
Решение. Даже и не ловко приводить решение 
Используем основное тригонометрическое тождество и учитываем, что синус отрицательный в 3-й и 4-й четвертях.
Если все-таки есть вопросы, то задавайте.
Ответ. -0.8.
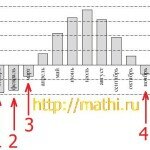
B8. На рисунке изображён график дифференцируемой функции y= f(x). Наоси абсцисс отмечены девять точек: x1, x2, x3, …, x9. Среди этих точекнайдите все точки, в которых производная функции f (x) отрицательна.В ответе укажите количество найденных точек.
Решение. На рисунке я галочками отметил точки, в которых производная меньше нуля. Это объясняется тем, что в указанных точках функция убывает. Таких точек 3, это и будет ответом.
Дополнительно отмечу, что в точках x3, x6 производная равна 0, т.к. одна из точек является точкой минимума, другая точкой максимума.
Ответ. 3
Связанные статьи
-
Решение задач b1-b4 демо по математике на 2012-й год
-
Решение задач b9, b10, b11 демонстрационного варианта по математике на 2012-й год
-
Демонстрационный вариант ЕГЭ по математике на 2012-й год
-
Решение задач b12, b13, b14 демонстрационного варианта по математике на 2012-й год
-
гиа по математике 2015 (демонстрационный вариант по математике) Часть 1
-
Демонстрационный вариант ЕГЭ по математике на 2011-й год
21 Май 2012 в 15:14
В8.
Как правильно определять точки, где производная функции отрицательна? Можно поподробней.
Точки максимума и минимума, я так понимаю, не используются… тогда как определить? Просто никогда не понимала до конца производные, да еще и на графике…
21 Май 2012 в 15:36
Производная функции отрицательна в тех точках, где функция убывает. Соответственно положительна, где функция возрастает. В данной задаче на отрезке [x3, x6] функция убывает, поэтому в точках x4, x5 производная отрицательна. По этому же принципу взята точка x9.
Производная же равна нулю в точках максимума и минимума. В данном случае это x3, x6 и неотмеченная точка между x8 и x9.
25 Декабрь 2012 в 14:46
круто! все понял в В8 пасиба!