Математика Решение заданий C2 ЕГЭ по математике

В ЕГЭ по математике 2013-го года задания с2 по прежнему содержит традиционную достаточно простую задачу по стереометрии. Рассмотрим примеры решений некоторых заданий с указанием возможных ошибок.

Критерии оценки

2 балла – обосновано получен верный ответ.

1 балл – Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ, решение не закончено или при правильном ответе недостаточно обосновано.

0 баллов – Решение не соответствует ни одному из критериев, описанных выше.

Приведу некоторые замечания по критериям оценки. Во-первых, рекомендуется проверять задания с2 достаточно мягко. Например, 2 балла может быть поставлено в том случае, если только описана и приведена правильная конструкция. Во вторых, вид ответа не должен влиять на оценку, т.е. если в ответах, предложенных Федеральной группой по математике, записан arcsin 0,6 , а выпускник написал 1/2 arcsin {24}/7 , то эксперт должен самостоятельно проверить равенство

arcsin 0,6=1/2 arcsin {24}/7 .

Замечу, что некоторые эксперты требуют, чтобы в ключах, выдаваемых при проверке, были перечислены все варианты, но это практически не реально.

Примеры решения задач c2 ЕГЭ по математике

1. 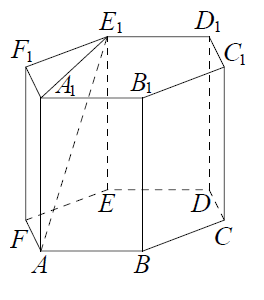В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки A до прямой E1D1.

Решение. По теореме косинусов

$AE^2=5^2 +5^2-2*5^2*cos {2pi}/3 =50+50*sin pi/6=75$

${AE_1}^2=AE^2+{EE_1}^2=75+11^2=196$

Следовательно искомое расстояние равно AE_1=14

Замечание по ошибкам 1. Может встретиться решение, состоящее из приведенного рисунка и только одной фразы:

Это расстояние равно AE_1=14

В данном случае подходит критерий “решение найдено, но недостаточно обосновано”, поэтому за это задание школьник все же получит 1 балл.

Замечание по ошибкам 2. Может оказаться так, что рисунок сделан правильно, ответ правильный, приведено решение. Но если при этом окажется, что в ходе решения допущены явные ошибки, то рекомендуется все же поставить о баллов. В данной задаче это может выражаться, например, в том, что школьник посчитает, что нужное расстояние это AD1, но потом сделает вычислительную ошибку и получит правильный результат.

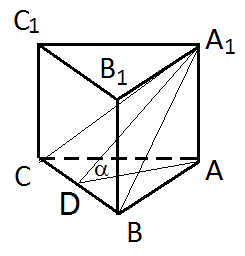2. Сторона основания правильной треугольной призмы ABCA1B!C1 равна 2, а диагональ боковой грани равна sqrt 5 . Найдите угол между плоскостью A1BC и плоскостью основания призмы.