Разбор задач с4 егэ по математике

Задача с4 егэ по математике посвящена геометрической задаче, в которой всегда существует два решения. Это связано с тем, что постановка задачи в одном из пунктов всегда имеет две трактовки. На это стоит всегда обращать внимание.

Критерии оценивания

3 балла – Рассмотрены все возможные геометрические конфигурации, и получен правильный ответ
2 балла – Рассмотрена хотя бы одна возможная конфигурация, для которой получено правильное значение искомой величины
1 балл – Рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой получено значение искомой величины, неправильное из-за арифметической ошибки
0 баллов – Решение не соответствует ни одному из критериев, перечисленных выше

Пример 1.

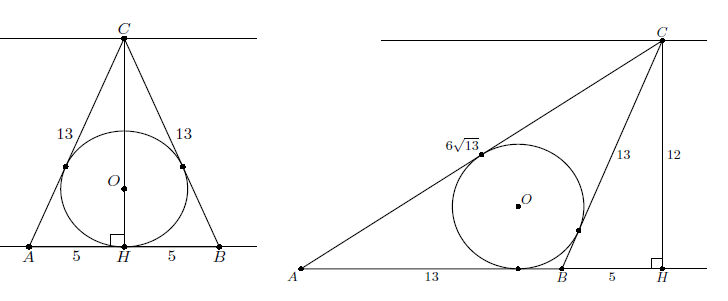
Расстояние между параллельными прямыми равно 12. На одной из них лежит точка C , а на другой – точки A и B,  причем треугольник ABC – равнобедренный и его боковая сторона равна 13. Найдите радиус окружности, вписанной в треугольник ABC .
Решение.

Заметим, что в данной задаче не сказано, какой отрезок является основанием, это может быть или отрезок AB, или AC. С учетом сказанного AC = BC или AB = BC.

Далее надо рассмотреть два случая. В первом случае (левый рисунок). AC = BC =13. Обозначим через H точку касания вписанной окружности треугольника ABC с основанием AB. Пусть r1 – радиус этой вписанной окружности.

Тогда CH – высота и медиана треугольника ABC . Из прямоугольного треугольника AHC находим, что .

Далее находим площадь треугольника . Но с другой стороны площадь треугольника может быть вычислена по формуле . Приравнивая площади треугольников получаем уравнение , из которого находим .

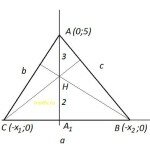
Во втором случае для определенности будем считать AB = BC =13 (правый рисунок). Пусть CH – высота треугольника ABC , r2 – радиус окружности, вписанной в треугольник ABC . Тогда BH = 5, AH = AB + BH =13 + 5 =18. Из прямоугольного треугольника ACH находим .

Аналогично как это было сделано в первом случае двумя способами находим площадь треугольника. С одной стороны Площадь равна . С другой стороны . Отсюда находим

Ответ: 

Замечание. Оценка не снижается, если результат не приведен к некому стандартному виду.

Распространенные ошибки

1. Рассмотрен только один вариант.

2. Может оказаться, что по ошибке правильно найден радиус описанной окружности вместо вписанной. К сожалению в этом случае ставят только 0 баллов.

3. Как следствие из второго пункта: Всегда внимательно читайте, что нужно найти.

4. Вычислительные ошибки. Или неверное применение формул. Например, в данном примере при вычислении площади треугольника использован не полупериметр, а периметр.

Задачи для самостоятельного решения

1. Расстояние между параллельными прямыми равно 4. На одной из них лежит точка C , а на другой – точки A и B , причем треугольник ABC – равнобедренный и его боковая сторона равна 5. Найдите радиус окружности, вписанной в треугольник ABC . Ответ: 1,5 или .

2. В треугольнике ABC AB =15, BC = 5 , AC =12 . Точка D лежит на прямой BC так, что BD:DC = 3: 4 . Окружности, вписанные в каждый из треугольников ADC и ADB, касаются стороны AD в точках E и F . Найдите длину отрезка EF .

Ответ:  или 4.

3. В треугольнике ABC AB =15, BC = 7, AC = 9 . Точка D лежит на прямой BC так, что BD:DC = 2 :3. Окружности, вписанные в каждый из треугольников ADC и ADB, касаются стороны AD в точках E и F . Найдите длину отрезка EF . Ответ: 6,5 или 3,7.

Приведем скриншот работы, получившей максимальные 3 балла.

4. В треугольнике ABC AB =13, BC = 7, AC =11. Точка D лежит на прямой BC так, что BD:DC =1: 7 . Окружности, вписанные в каждый из треугольников ADC и ADB, касаются стороны AD в точках E и F . Найдите длину отрезка EF . Ответ: 4,5 или 29/8.

5. В треугольнике ABC AB = 9, BC = 5 , AC = 8. Точка D лежит на прямой BC так, что BD:DC = 3: 7 . Окружности, вписанные в каждый из треугольников ADC и ADB, касаются стороны AD в точках E и F . Найдите длину отрезка EF . Ответ: 1,5 или 3.

6. В треугольнике ABC AB =14, BC =10 , AC =12 . Точка D лежит на прямой BC так, что BD:DC = 3: 7 . Окружности, вписанные в каждый из треугольников ADC и ADB, касаются стороны AD в точках E и F . Найдите длину отрезка EF . Ответ: 3 или 6.