Пример построения графика функции

При решении задач с параметрами нередко необходимо построить график функции, после чего задача практически сразу решается. При построении графика функции рекомендуется придерживаться следующей схемы исследования.

Построение графика функции

1. Найти область определения.
2. Выяснить, есть ли особенности функции (четность-нечетность, периодичность).
3. Найти точки пересечения с осями.
4. Найти промежутки возрастания-убывания функции, экстремумы.
5. Найдите значение функции в точках экстремума.
6. Выясните поведение функции при больших x (т.е. определите, есть ли асимптоты).
7. Постройте график.

Построим график функции в соответствии с предложенной схемой.

1. Область определения – вся числовая прямая.

2. , т.е. y(x) – нечетная функция – ее график будет симметричен относительно начала координат.

3. (0,0) – единственная точка пересечения с осями.

4. Найдем производную:

‘=,

Приравнивая производную к 0, получаем точки 

Отметим эти точки на координатной прямой

Далее расставляем знаки производной и отмечаем промежутки возрастания и убывания. При этом получаем, что – точка максимума,  – точка минимума.

5. Определим значения функции в точках экстремума:

– точка

6. Заметим, что при стремлении x к бесконечности функция стремиться к 0.

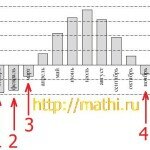
7. Учитывая проведенное выше исследование функции, строим график как показано ниже.

 

 

Задачи с параметрами

Приведем пример задачи с параметрами, в которой важно уметь строить графики.

Определить значение параметра a, при котором уравнение  имеет единственное решение.

Решение. Обозначим правую часть через f(x), правую часть через g(x). График функции f(x) показан на рисунке выше. g(x) представляет собой семейство прямых параллельных оси 0x. Заметим, что функции f(x) и g(x) пересекаются при a=-1, 0, 1. Это и будет ответом.